Beyond All Reason est un super RTS et descendant de Total Annihilation 🤖 Le jeu est basé sur le moteur Recoil (précédemment SpringRTS) et donc entièrement open source, le rendant doublement intéressant puisqu’on peut directement participer à l’améliorer.
Comme sur tous les jeux RTS classiques, un des modes de jeu disponibles est le FFA jusqu’à 16 joueurs (extrêmement fun). Dans ce mode de jeu, les joueurs se voient automatiquement attribués une position de départ au lancement de la partie, et j’était légèrement frustré par le manque de flexibilité du système : en bref, un ensemble statique de points de départ est défini sur chaque carte, et au lancement de la partie, le système sélectionnait les X premiers points et les attribuait aléatoirement aux joueurs.
En pratique, au lancement d’un FFA à 12 joueurs sur une carte avec 16 positions, le jeu choisissait systématiquement les positions de départ 1 à 12, et donc les positions de départ pour 12 sur cette carte étaient toujours les mêmes, les positions 13 à 16 n’étant jamais utilisées. J’ai décidé de l’améliorer en ajoutant la possibilité de définir plusieurs dispositions pour X joueurs par carte, donnant ainsi plus de flexibilité dans la définition de dispositions équitables et imprévisibles pour différentes tailles de FFA sur une même carte.
En guise d’illustration, la carte suivante permet de jouer des matchs FFA équitables de différentes tailles (3 joueurs, 5 joueurs, 7 joueurs, etc.) grâce à son design à triple cercles concentriques. Cependant, le système par défaut n’était pas suffisamment flexible pour permettre de jouer à 3 ou à 5 vu qu’il sélectionnait toujours les X premiers points pour X joueurs, résultant en des positions de départ inéquitables. Le nouveau système résout ce problème en définissant des dispositions appropriées pour toutes tailles de FFA.
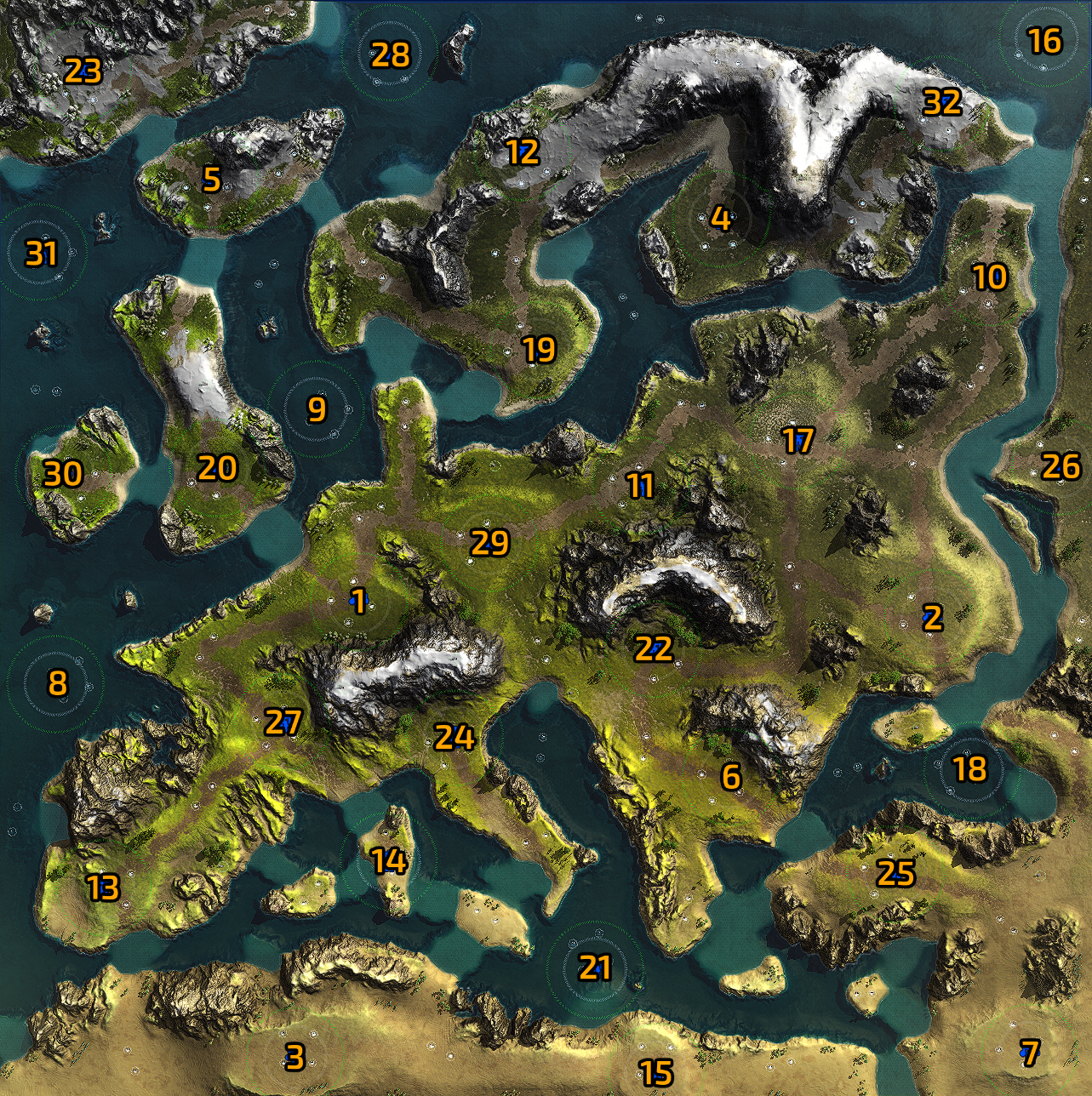
Celles-ci furent faciles à définir sur la plupart des cartes, comme dans l’exemple ci-dessus, mais bien sûr ce ne fut pas le cas pour toutes, et notamment pour les cartes asymétriques. L’une d’elles en particulier est unique car c’est la seule carte du jeu avec plus que 16 positions de départ : elle en a 32.
Étant donné que des ressources stratégiques sont disponibles sur chaque point de départ, il faut veiller à répartir les joueurs de telle sorte qu’aucun n’ait accès à considérablement plus ou moins de ressources qu’un autre, ce qui peut naïvement être fait en essayant d’éviter que 2 joueurs ne démarrent l’un à côté de l’autre. Mais essayer de déterminer manuellement des dispositions équitables sur cette carte était un cauchemar, et pour cause, compte tenu du nombre de 16-combinaisons possibles sur 32 points de départ :
\[ C(32, 16) = {32 \choose 16} = {\frac{32!}{16!16!}} = 601\,080\,390\]
J’ai donc décidé d’utiliser la théorie des graphes pour m’aider. La carte peut être représentée sous forme de graphe où chaque point de départ est un nœud et le voisinage est matérialisé par une arête :
Partant de là, on peut :
- Rechercher des stables de cardinal maximum, c’est à dire des ensembles de positions de départ tels qu’aucunes des positions de départ ne soient adjacentes et où aucune autre position de départ ne puisse être ajoutée sans perdre cette propriété. In fine, ce sont des dispositions de joueurs qui peuvent être utilisées telles quelles.
- Identifier les cliques, c’est-à-dire des ensembles de positions de départ qui sont toutes adjacentes les unes aux autres. Celles-ci peuvent être utilisées pour identifier des variations possibles sur une disposition de joueurs existante, et en créer de nouvelles.
À l’aide d’un peu de Python et de NetworkX, ce fut très facile :
Après un peu de nettoyage et quelques contraintes supplémentaires (pour essayer d’éviter certaines positions moins désirables), je me suis retrouvé avec un lot de stables de cardinal maximum allant de 8 à 12 nœuds, qui ont été utilisés pour l’amorçage des dispositions de 8 à 12 joueurs. À partir de là, les dispositions de 3 à 7 joueurs ont été dérivées en supprimant et en remaniant progressivement les points de départ des dispositions à 8, tandis que les dispositions à 13 et plus ont été dérivées en utilisant les dispositions à 12 et les cliques comme référence. Voici un exemple de stable de cardinal maximum utilisé pour une disposition à 12 joueurs :
Merci la théorie des graphes 👌