Beyond All Reason is an awesome RTS descended from Total Annihilation 🤖 The game is based on the Recoil engine (formerly SpringRTS) and thus entirely open source, which makes it doubly interesting as players can directly participate in improving the game.
As on all classic RTS games, one of the available game modes is FFA up to 16 players (extremely fun). In this mode, players are automatically assigned a start position at game start, and I was slightly annoyed by the system’s inflexibility: in a nutshell, a set of static start points is defined on each map, and on game start the system would pick the first X points and randomly assign them to players.
In effect, when starting a 12-way FFA on a 16-position map, the game would systematically pick start positions 1-12, meaning the start positions for a 12-way on this map would always be the same and positions 13-16 would never be used. I set out to improve this by adding the possibility to define multiple layouts per X-way per map, thus allowing for more flexibility in defining fair and unpredictable layouts for various sizes of FFA on the same map.
To illustrate, the following map allows to play fair FFA matches at various sizes (3-way, 5-way, 7-way, etc.) thanks to its clever triple-concentric-rings design. However, the default system was not flexible enough to actually allow it to be played in 3-way or 5-way as it always picked the first X points for X players, resulting in unfair start positions. The new system addresses this since appropriate layouts for all FFA sizes can be defined.
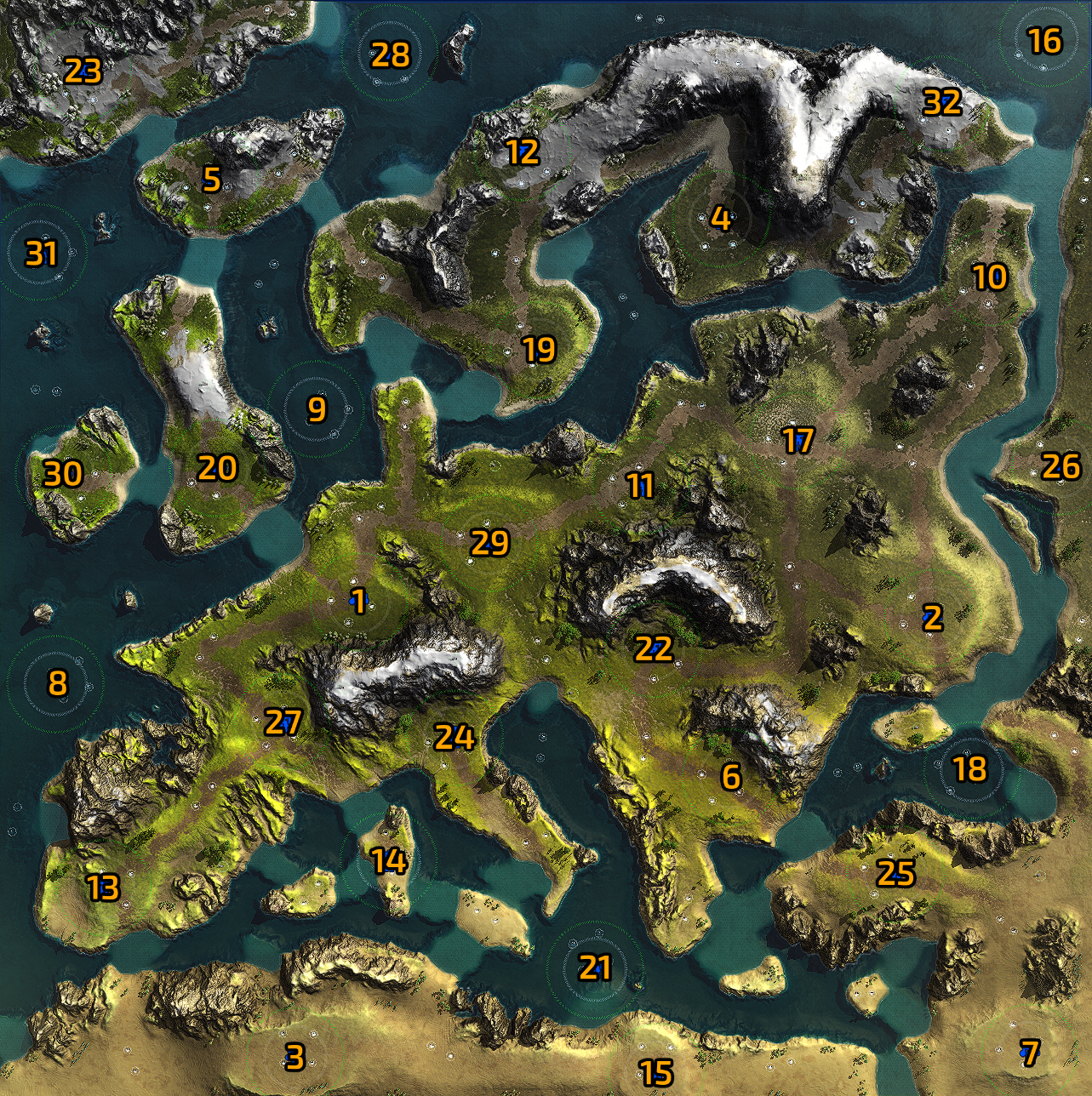
Proper layouts were as easy to figure out on most maps as in the example above, but of course some proved to be challenging, and notably asymmetrical maps. One of them in particular is unique because it is the only map in the game with more than 16 start positions: it has 32.
Since strategic resources are available on each start point, attention should be paid to distributing players such that none has access to considerably more or less resources than another, which can naively be done by trying to avoid having 2 players starting next to each other. But trying to manually figure out fair layouts on this map was a nightmare, and for good reason considering the number of 16-combination possible out of 32 start points:
\[ C(32, 16) = {32 \choose 16} = {\frac{32!}{16!16!}} = 601\,080\,390\]
So I decided to use graph theory to help me out. The map can be represented as a graph where each start point is a node and neighbour status is materialized by an edge:
From there, we can:
- Search for maximal independent sets, i.e. sets of start positions such that no start positions are adjacent and where no further start position can be added without losing that property. These are basically FFA layouts that can be used as-is.
- Identify cliques, i.e. sets of start positions which are all adjacent to each other. These can be used to identify possible variations on an existing layout and help creating new layouts.
And thanks to some Python and NetworkX, this was very easy to do:
After some filtering and some additional constraints (to try and avoid some positions which are less desirable), I was left with a batch of maximal independent sets ranging from 8 to 12 nodes, which were used for seeding layouts from 8-way to 12-way. From there, layouts down to 3-way were derived by progressively removing and reshuffling start points downwards from 8-way, while layouts for 13-way and up were derived by using 12-way layouts and cliques as reference. Here’s one example of a maximal independent set used as a 12-way layout:
Thank you graph theory 👌